贾宪创造的增乘开方法,又称递增开方法,把开方技术推进到一个新的阶段。目前中学数学教科书中的综合除法的程序与此相类似。它主要用随乘随加代替一次使用贾宪三角的各廉。我们以开1336336的四次方(古代称为三乘方)为例说明之。
图30 朱世杰改进的贾宪三角
递增三乘开方法草曰①:(1)置积为实。别置一算名曰下法于实末。常超三位,约实。〔一乘超一位,三乘超三位。万上定实。〕
(2)上商得数〔三十〕;乘下法,生下廉〔三十〕;乘下廉,生上廉〔九百〕;乘上廉,生立方〔二万七千〕。命上商,除实〔余五十二万六千三百三十六〕。(3)作法:商第二位得数。以上商乘下法,入下廉〔共六十〕;乘下廉,入上廉〔共二千七百〕;乘上廉入方〔共一十万八千〕。(4)又乘下法入下廉〔共九十〕;乘下廉入上廉〔共五千四百〕。又乘下法入下廉〔共一百二十〕。(5)方一、上廉二、下廉三、下法四退〔方一十万八千,上廉五千四百,下廉一百二十,下法定一。〕。(6)又于上商之次续商置得数〔第二位:四〕。以乘下法入下廉〔一百二十四〕;乘下廉入上廉〔共五千八百九十六〕,乘上廉并为立方〔一十三万一千五百八十四〕。命上商,除实,尽,得三乘方一面之数[如三位立方,依第二位取用]。
其计算草图应为:
这是有文字记载的第一个开四次方程序,它比立成释锁法简便。这个开方如果不用随乘随加,便要利用贾宪三角第五层,计算4·3,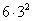 ,
,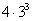 。同时,它的程序化比立成释锁法更强,只要作好第一步布位定位,掌握退位步数,那么以商自下而上递乘递加,每低一位而止,对任何次方都相同。开方次数愈高,商的位数愈多,数字愈大,就愈显得这种方法优越。后来在阿拉伯地区产生了同样的方法。而在欧洲,直到上世纪初才先后由鲁菲尼与霍纳创造出来,故称为鲁菲尼—霍纳法或霍纳法,比贾宪晚800余年。
。同时,它的程序化比立成释锁法更强,只要作好第一步布位定位,掌握退位步数,那么以商自下而上递乘递加,每低一位而止,对任何次方都相同。开方次数愈高,商的位数愈多,数字愈大,就愈显得这种方法优越。后来在阿拉伯地区产生了同样的方法。而在欧洲,直到上世纪初才先后由鲁菲尼与霍纳创造出来,故称为鲁菲尼—霍纳法或霍纳法,比贾宪晚800余年。
——————
注释:
①此为法、草合一,原以大、小字区别,今将草放入方括号中。以下的(1)、(2)、(3)、……是作者加的,以便与下图相应。
(穷奇网 www.71101.net)