刘益《议古根源》根据已知“直田积864步，只云长阔共60步”，连续提出两个问题，一是“欲先求阔步得几何？”一是“欲先求长步，问得几何？”显然此二问都归结到同一方程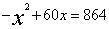，它的两个根x1=24，x2=36便分别为这两个问题的答案。但是刘益和杨辉都未能从这一例子认识到二次及其以上的方程可能有多于一个的正根，并进而讨论根与系数的关系问题。直到清中叶中国古典数学复兴，汪莱、李锐才考虑这个问题，取得了杰出的成就。汪莱1801年在《第五册算书》中首先提出二次方程可能有一个或二个正根，三次方程可能有一个、二个或三个正根。秦九韶、李冶书中的方程有许多不只一个正根，不加分析地取其中一个为答数是不应该的。例如，形如
　

　　的几个方程如有正根，便不只一个，而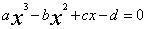的正根可能是一个，可能是三个。他还明确指出，如x1，x2，x3是其正根，则。

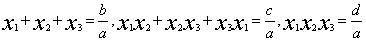　　汪莱初步考虑了正根个数与方程系数正负号的关系。汪莱从六安将《第五册算书》寄给扬州焦循，次年焦循携书到杭州与李锐共同研究。李锐将汪莱对二、三次方程正根的研究推广到任意高次方程，提出了三条判别根与系数关系的法则，把这项研究提高到一个新的阶段。然而三条中第二条有语病，汪莱举出了一个反例。他们对这一问题继续研究。后来李锐撰《开方说》，提出：方程系数符号变化一次的常有一个正根，变化二次的有二正根，变化三次的有三正根或一正根，变化四次的有四正根或二正根。正根个数比符号变化次数少时，所缺少的根就是汪莱所说的“无数”，它们必定成对，没有缺一根的情形。李锐这一判别法则与欧洲17世纪笛卡儿的符号法则是等价的。

　　李锐还承认方程的根可以是负数，用增乘开方法求负根的方法与求正根一致。他认为，求出一个根之后，可用此根将方程降低一次以求第二个根，如此逐步降幂，而不必就原方程开方。李锐还首次提出方程有重根的问题。至此，中国的方程论形成了一门比较完整的学科
（穷奇网　www.71101.net）