欧洲现代数学大师欧拉(公元1707—1783年)、拉格郎日(公元1736—1813年)都对同余式问题作过研究。高斯(公元1777—1855年)的《算术探究》(公元1801年)中明确写出了上述定理。来华传教士伟烈亚力(公元1815—1887年)1852年将“物不知数”题介绍到西方，人们发现它与上述定理一致，遂称之为中国剩余定理。
同余式解法还来自于历法制定中上元积年的计算。中国古代的历法，要假定远古有一个甲子日，那一年的冬至与十一月的合朔都恰好在这一日的子时初刻。有这么一天的年度叫上元，从上元到制定历法的本年的总年数叫上元积年。已知本年冬至时刻及十一月平朔时刻，求“上元积年”在数学上便是同余式问题。但是，“历家虽用，用而不知”(《数书九章序》)，在中国数学史也是世界数学史上第一次提出一次同余式组完整解法的是南宋数学家秦九韶。
秦九韶的方法称为大衍总数术。他将诸ki叫作乘率，诸Ai叫作定数，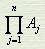
叫作衍母，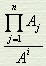
叫衍数，而方法的核心是大衍求一术，即求乘率ki的方法。为叙述方便，我们将
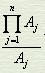记为G，将Ai记为A，ki记为k，求一术变成在A、G互素的情况下求满足kG≡1 (modA)的k值。秦九韶首先提出，如果G>A，若G≡g(modA)，0 < g < A，则kg≡1
(modA)与kG≡1(modA)等价，这便是现代同余式理论中的传递性。因此问题变成了求满足kg≡1(modA)的k。秦九韶称g为奇数。他的大衍求一术是：将g置于右上，A置于右下，左上置天元一，g与A辗转相除，商依次是q1、q2……余数是r1、r2……按一定规则在左下、左上计算c1、c2……直到右上rn=1为止(此时n必定是偶数)，则左上的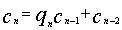
便是所求的k值。用现代符号表示就是：
这里要计算到右上rn=1，故有“求一”之名。可以证明，这种求乘率k的方法是正确的。在上述方法中，诸Ai必须是两两互素的正整数，但是在实际问题中诸Ai不一定互素，甚至不一定是整数，可能是分数或小数。秦九韶针对不同的情况，提出了化约各种不同的问题为定数的程序。由于中国古代没有因数分解的概念，化约过程走了弯路，但毕竟比较成功地解决了这个问题。
秦九韶把大衍总数术不仅用于历法推算，而且用于建筑、行程、粟米交易、库额利息，甚至断案等问题。谨以“余米推数”问为例。有一米铺投诉被盗去三箩筐米，不知数量。左箩剩1合，中箩剩14合，右箩剩1合。后捉到盗米贼甲、乙、丙。甲说，当夜他摸得一只马杓，一杓杓将左箩的米舀入布袋；乙说，他踢着一只木履，将中箩的米舀入布袋；丙说，他摸得一只漆碗，将右箩的米舀入布袋。三人将米拿回家食用，日久不知其数，遂交出作案工具。量得一马杓容19合，一木履17合，一漆碗12合。问共丢失的米数及三人所盗的米数。这是求同余式组的解N。
N≡1 (mod 19)≡14(mod 17)≡1 (mod 12)
由于19、17、12两两互素，便为定数。衍母为19×17×12=3876，衍数依次是17×12=204，19×12=228，19×17=323。求分别满足k1×204≡1
(mod 19)，k2×228≡1 (mod 17)，k3×323≡1(mod
12)的乘率k1，k2，k3。由于衍数分别大于定数，便用定数减衍数，得奇数14，7，11。问题变成求分别满足k1×14≡1 (mod 19)，k2×7≡1
(mod 17)，k3×11≡1 (mod 12)的k1，k2，k3。求k1的程序：
求k2的程序：
求k3的程序：
于是 N≡1×15×204+14×5×228+1×11×323(mod3876)≡22573(mod3876)=3193.
每箩米数3193合，甲、丙盗米各为3192合，乙盗米3179合，共盗米9563合。
——————
注释：
①
（穷奇网 www.71101.net）